☛ Activité préparatoire - Énoncé

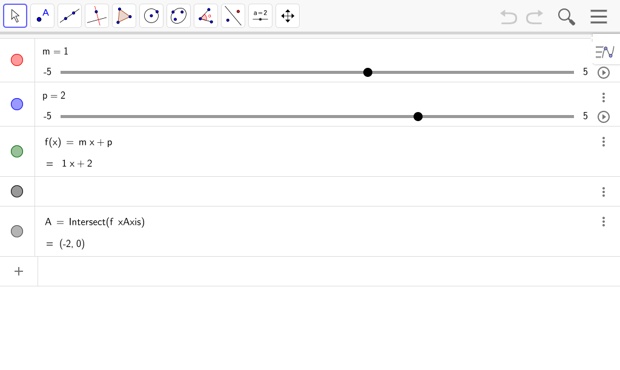
Soit \(m\) et \(p\) deux réels. On considère la fonction affine \(f\) définie sur \(\mathbb{R}\) par \(f(x)=mx+p\).
Voici sa droite représentative \(\mathcal{D}\) dans un repère du plan.

1. Fixer une valeur de \(m\). Faire varier le curseur \(p\) et conjecturer l'effet de ce coefficient sur la droite \(\mathcal{D}\).

2. Fixer une valeur de \(p\). Faire varier la valeur de \(m\) et conjecturer le sens de variation de la fonction \(f\) sur \(\mathbb{R}\).

3. Dans cette question on suppose que \(m=0\). Que peut-on dire de l'équation \(f(x)=0\) ?

4. Dans cette question on suppose que \(m\neq 0\).
    a. En faisant varier la valeur de \(m\), déterminer le nombre de solutions de l'équation \(f(x)=0\).
    b. Conjecturer le signe de \(mx+p\) sur \(\mathbb{R}\) en fonction de \(m\).